Maple is a robust math environment which can graph, solve equations, and solve for the unknown with the aid of its computer algebra solver (CAS), which is capable of computing exact roots of cubic functions, for example.
I wanted to demonstrate for myself that Maple could do various function transformations, such as: f(x), f(x + 1), f(x) + 1, 2*f(x), and the like. I discovered after much reading and browsing the web that I could coax f(x) to do whatever is needed using an inline call:
f := proc (x :: float) option inline;
x4 + 5x3 + 5x2 - 5*x - 6
end proc:
The function takes a floating point number x as a parameter. This means that f(-10.0) would yield
5544.0000
as output. I noticed that Maple practices fairly strong typing, so if you declare floating point using float, you can only pass floats to the function. That is, f(-10) would have gotten an error, at least in my copy of Maple 12. Once you execute this proc declaration, you can do a plot function like:
plot ({f(x), f(x + 1), f(x + 2)}, x = -5..5, numpoints=1000);
and superimpose three curves on the same set of axes to make a comparison. You can even do:
plot ({f(x), 0.5 * f(2*(x + 1)) - 5}, x = -10..10, numpoints=1000);
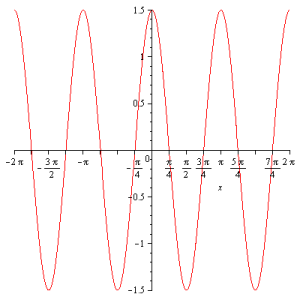
to illustrate combinations of transformations of a function. Even a transformation of a sine wave can look like this:
h := proc (x::float) option inline;
sin(x)
end proc;
plot(1.5h(2(x+Pi/4)), x = -2Pi .. 2Pi, numpoints = 5000, tickmarks = [spacing((1/4)*Pi), default]);
and you are rewarded with:
There is an even better function called animate which is great for transformations of functions. I will discuss that in a later post.
Visits: 91
