Notice that to show the rules for making these kind of magic squares, I used only odd-ordered square matrices as examples. What about matrices of even numbers of rows and columns? The rules for these vary.
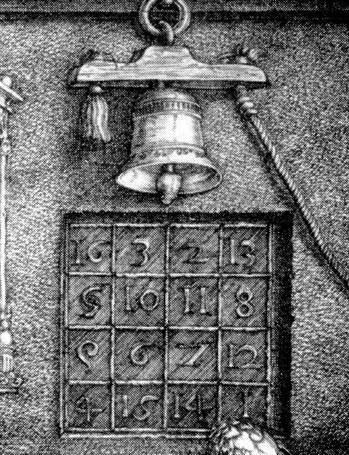
The famous Durer magic square, with the year of the engraving cleverly made a part of a magic square, has a certain organization in its construction, as well as a certain symmetry. The numbers are constructed, in sequence:
_ 3 2 _ _ 3 2 _ _ _ _ _ 5 _ _ 8 _ _ _ _ ====> _ 6 7 _ 4 _ _ 1 4 _ _ 1 _ 3 2 _ 16 3 2 13 5 10 11 8 5 10 11 8 9 6 7 12 ====> 9 6 7 12 4 _ _ 1 4 15 14 1
So, you start from the bottom right and proceed in a horseshoe to the top then the bottom left. The next diagram places the numbers 5-8 in a pattern that is left-to-right u-shape. Then the same u-shape for the numbers 9-12 from left to right, except this time it’s upside-down. Finally ending as we started, the same horseshoe shape (except right side up) from right to left.
Durer’s square has many things about it, apart from its magic number (34) which works on all the attendant diagonals, rows and columns. The middle 4 squares add up to 34 (10 + 11 + 6 + 7 = 34); the four corners add to 34 (16 + 13 + 4 + 1 = 34), and all corner foursomes add to 34: (16 + 3 + 5 + 10); (2 + 13 + 11 + 8); (9 + 6 + 4 + 15); and (7 + 12 + 14 + 1).
The numbers at the ends of the two middle rows add to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
and the numbers at the tops and bottoms of the two middle columns add to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
If we take another symmetrical combination: a rightward-slanting rectangle whose corners are 2, 8, 9, and 15, these also add to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
The leftward-slanting rectangle, whose corners are 5, 3, 12, and 14 also add to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
Starting from 2 and proceeding in an “L”-shape to the left to the number 5, and continuing counter-clockwise in the same manner gets us the corners of a tilted square whose numbers 2, 5, 15, and 12, add to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
Starting from “3” and doing likewise yields the numbers 3, 9, 14, and 8, also adding to 34:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
And what about this talk about “symmetry”? By this, we mean that we may take pairs of numbers at the start and end of any row, and they add up to the same number in a symmetrical place elsewhere. 16 + 3 = 4 + 15, taking the top and bottom of the first and second column. Likewise can be done for the last two columns: 2 + 13 = 14 + 1. The middle two rows have the same property: 5 + 10 = 9 + 6; and 11 + 8 = 7 + 12. On a larger scale, the sums of the middle two rows of columns 1 and 2 are the same as the tops and bottoms of columns 3 and 4: 11 + 8 = 7 + 12 = 16 + 3 = 4 + 15. Likewise, the sums of the middle two rows of columns 3 and 4 are the same as the tops and bottoms of columns 1 and 2: 2 + 13 = 14 + 1 = 5 + 10 = 9 + 6. These two groups of symmetrical numbers are illustrated below in red and green:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
The sums of 15 (green) and 18 (red) across each row form this pattern
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
The downward symmetry is also interesting. Here, the sum of 25 is in gold and the sum of 9 is in blue. In the process, we can discern the patterns that we used to construct the square in the first place:
16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
This is an incredible amount of magic, but if you follow the order of filling (horseshoes are right-to-left, u-shapes are left-to-right, along with the peculiar pattern of filling u’s and horseshoes), there really are four possible patterns that have these “hyper-magic” qualities, but you lose the “1514” idea in two of them:
8 11 10 5 12 7 6 9 4 15 14 1 13 2 3 16 1 14 15 4 12 6 7 9 1 14 15 4 13 2 3 16 5 11 10 8 12 7 6 9 8 11 10 5 16 3 2 13
Of course, you could reverse all of the numbers in the rows of the first two squares to get your “1514” back.
Every time I look at that darned Durer square, I keep seeing more patterns. I think there comes a point where one has to leave the remaining observations up to the reader.
There is yet another 4×4 square, and with it we can increase the magic, if that can even be conceivable after all I have said. But there is a square with even more magic than the Durer square. R. J. Reichmann mentioned it in his book “The Fascination of Numbers”, first published in 1957. The square could be constructed like this:
- - 3 - - - 3 6 - 10 3 6 15 10 3 6 4 - - - ====> 4 5 - - ====> 4 5 - 9 ====> 4 5 16 9 - - 2 - - - 2 7 - 11 2 7 14 11 2 7 1 - - - 1 8 - - 1 8 - 12 1 8 13 12
This square has all the magic of the Durer square and then some. One thing this new square has over the Durer square is that any four numbers in square formation will add to 34, from anywhere in the square. These include the foursomes:
10 3 16 9 11 2 4 5 5 16 2 7 8 13 14 11
Visits: 86
