Category: Science and Technology

What is old is new: RPN on the HP 35s Scientific Calculator part 3

The print-edition of the HP 35s manual

For those of you lucky enough to purchase the calculator back in 2007, you more than likely had the full 200-page print edition of the user manual. HP discontinued the print edition, possibly later that same year. It has been replaced by a smaller 40-page mini manual whose only real useful purpose has been to help me review the main points of RPN. If you are a beginner, then you need to access the full manual which is now stored on CD. My CD, which I bought less than a week ago, appears to have been last updated in 2009. The same CD also has the same manual in 15 other languages.

You would have had the ability to review the book at your leisure, rather than on a laptop screen the way I have to view it. It is a bit of a deterrent and is tiring on my eyes, but I guess it beats having no book. I have discovered that you can purchase copies on E-Bay if you feel desparate enough for a print copy. You will probably shuck out your dollars for a print copy if you want to program, or if you want to have a more through mastery of its system of menus.

However, if you program, it must be stated quickly that much of the programming language is printed on the keyboard above the keys, and are active in program mode. It is definitely a caclulator that had its keyboard laid out with the programmer in mind, and with their needs as the higher priority. A look at the keypad shows a lot of programming commands rather than statistics, summations, or clearing the stack, all of which require menus. The “STO” function requires the blue shift key to be pressed first; and the functions for x2, log, ln all require a shift key to be pressed first. For whatever reason that perplexes me, there seemed to be a need to cram a good fraction of the interface of the calculator with various conversions: metric to imperial, fraction to floating point, degrees to radians, signed to absolute value. It takes up 10 of the 43 keys. Since none but grade-school calculators have these conversions, I am not sure of the motive. It is likely that it helps in the programming to save coding effort.

It seems to be all about the programming. Programming takes up 5 chapters or 100 pages of the 382-page booklet. Plenty to learn for the HP 35s programming enthusiast.

Visits: 73

What is old is new: RPN on the HP 35s Scientific Calculator part 2

I saw the 35s for the first time in a Staples store just this year, though the calculator has been around in University bookstores since 2007. I bought mine on sale, being listed at $99.00 full price. When it came out in 2007, I heard that it came with a zippered pouch to store the calculator in. Mine, supposedly the 2011 model, came with a vinyl pouch that was open, with rather stiff elasticized cloth bands on the sides, making the calculator difficult to actually place in its pouch, especially the first time it was used.  Once in the pouch, it was difficult to take back out of its pouch. The calculator feels light when held in one’s hand. I’m not sure why I noticed that. Somehow I thought it would feel more substantial, given all of the functions and programmability, and the 800 or so memories that it boasts of.

2012 will be the 40th anniversary of the scientific calculator. HP made the world’s first scientific calculator in 1972, and it was an RPN calculator with no algebraic mode. Anyone who has tried to program in a serious way would appreciate that RPN is easier to program for (from the manufacturer’s point of view), because of its reliance on a memory model called “stacks”, which most computer science undergraduates know about, by second year at the latest. While the act of doing things algebraically might seem easier to us humans, programming a calculator to think in terms of human algebra is more difficult than you would think. It takes a computer many more steps, and thus it is much slower than RPN in terms of processor time. It was probably not until the early 1990s that calculators were capable of anything close to human-style algebra, and only recently have processors become so small and fast that the speed of the algorithm is not really as important as it used to be. But human speed might be. To those who take the time to understand how RPN works, and how the 35s implements stacks, RPN is still faster for humans to perform calculations.

Many of the features on the 35s are common on much cheaper calculators: statistics, regression, vectors, mixed fractions, complex numbers, numerical integration, numerical differentiation, a linear solver, and there are much cheaper calculators that can solve single-variable polynomials up to order 3. I own a $5.00 calculator that can solve linear systems in up to 3 unknowns. Also, there are too many features on the “new” HP 35s that are tied up in menus, which is something that turned me off from using TI calculators. The only tangible attraction I can think of for this calculator is likely to be its programming mode. The 35s is among the very few non-graphical calculators around today that one can write programs in.

Playing with it a bit, I find that scientific notation seems to work up to 10500, meaning the computation of factorials can go to unheard-of extremes, even going beyond the capacity of an Excel spreadsheet. I was able to find, to several sig figs, the value of 253!, wheras Excel 2007 craps out past 125!. This means that this calculator is particularly powerful for performing permutations (nPr) and combinations (nCr).

I have lost my touch with the use of stacks from my programming days, but it looks like the calculator does a lot of pushing and popping, even in the middle of the stack. In addition, it only seems to perform calculations on the stack 2 at a time, even though the stack can accomodate 4 numbers. When you enter numbers, it’s like “pushing” numbers on to the bottom of the stack. You enter a number, and the stack moves up. If  you enter two numbers then add them, the stack moves down and the result of the addition is entered in the immediate register in the stack, called “x”.  The true implemtnation of this is that, for the registers t, z, y, and x, t gets its number copied to z, z copies to y, and y copies to x. This results in a duplication of t in the stack. If a “+” is pressed when a stack contains the numbers “1 2 3 4”, it adds only 3 and4, then the top 2 registers shift down and the result of adding 3 and 4 is placed in “x”: “1 1 2 7” becomes the resulting stack. The “1” and “2” shift down, but in reality, the memory register values are just copied.

Visits: 114

Microphones Part 2: The war of silence

With the levels down so low, my test recording needed post-processing. I used Adobe Audition 1.5. In most of these audio-doctoring softwares, all you need to do is to normalize the levels, so that “0” is the highest your levels should go. Audition had a “Normalize” setting, and of course that also boosted the background and electronic noise, along with my voice.

Now I needed noise reduction. Adobe has a fancy dancy noise reduction interface which is useable for the brave of heart. The main idea is to highlight “silence” (a moment of pure background noise) somewhere on your waveform, in order for Adobe to get a snapshot of the frequencies that need to be attenuated with the noise reduction. When I tried it, the noise was virtually eliminated when there was only noise, especially at the start, but the noise seems to have a reverberation, since if the noise is at the end, it fades in a stepwise fashion. The noise in the middle is reduced substantially, but not enough to compare with other noise reduction that I know about, like Dolby or ANRS. DBX would have been good, if they could have licensed it.

Audacity won the war of silence, in making the background noise pretty much inaudible, with its noise reduction scheme, which had a far simpler interface. The noise reduction was equally effective in the silent bits and the parts with talking. I used the same strategy in giving it a sample of pure background noise to its noise reduction profile. I found that only the very lowest setting on their “Less/More” slider would not make me sound like I’m living in a tin can, or even disappear altogether.

To be fair, I was using Audition 1.5, against the latest version of Audacity. I hear that Audition is somewhere around version 3.0. But I am happy with Audacity, since Adobe charges a pretty penny for its sound editing software.

Visits: 83

Microphones

I had decided to do my little contribution to society, and join LibriVox.org, and record a free audio file for them. My biggest problem so far has been microphones. I have an Optimus mike that was purchased 5 years ago, and had hardly been used. I had decided to use it for LibriVox, but my first problem was in finding an adaptor, since the Optimus uses a quarter inch plug, and my sound card has only eighth-inch jacks.

I went to The Source (which used to be Radio Shack), and got two adaptors, one mono and one stereo. The stereo adaptor I purchased fell apart inside the jack, and I almost took the front end of the computer off trying to dislodge it. First, the sheath came off, leaving the bare plug, stripped of its barrel with its bare contacts hanging in the air. With a pair of pliers, I managed to remove the rest of the plug. But when that happened, I noticed that one of the insulators on the plug was stripped off. I checked the package. Made in China. !@*#$ free trade agreements! @!#@$$#$@!! global economy!

I took a chance on the Chinese-made mono plug, and Buddha smiled on me for that one, for it seemed to work fine. Trouble was Windows didn’t know it was there, so I tried the back. That was fine, but the levels were too quiet, even with the Windows levels turned all the way up.

Visits: 75

Kudos to the 1050 CHUM Memorial Blog

Recently, I’ve been hit (my website that is) by someone possibly checking his plethora of links from his/her website, and when I back-traced it, I find this cool blog which acts as a convincing historical shrine to the late great 1050 CHUM Radio in Toronto. I’ve written about it before, and had mourned the reduction of a once-powerful music station to nothing more than an on-air feed for an all-news cable TV station.

There are some bugs to iron out with this blog.  While the content is excellent, and is a great cross-section of its 50-year history, there is little need to cram everything on to one nearly interminable page. I would go for short pages. Many short pages. Dozens. Hundreds of short pages. Yes, we know its history is long and illustrious. It was the home of The Chum Charts, and, was the place where countless celebrities made their appearance. Even spending part of my childhood in rural Saskatchewan was not enough to escape the annual Top 100 countdown piped to a local station in town from that seminal station near Yonge St. and Eglinton and DJ’ed by people like Bob MacAdorey. And we know there is a lot to archive: 50 years of sound checks, CHUM charts, and paraphernalia can do that, to say nothing of links to other sites which have articles possibly written by other CHUM fans, making their own contribution.

Visits: 66

The Psychology Contrarian II: The Obsession with IQ

At best, these websites present these people as numbers first, people second. To what extent does saying that Marie Curie has an IQ of 190 or so add to or take away from her discovery of radioactivity or her other contributions to Chemistry and Physics to which she literally paid for with her life, all the while fleeing the Nazis? To what extent does Shakespeare’s assigned IQ of 210 add to or take away from his being the most quoted writer in the English Language? And finally, just who is this guy “William Sidis”, and who in the h-e-double-sticks gave him an IQ of 250 to 300?

William Sidis (1898-1944), was an American who had an undergraduate degree at MIT, and then a studied for a law degree at Harvard before he reached 18. By that time he had given occasional lectures to professors. He was portrayed as Will Hunting in the 1997 movie Good Will Hunting. But Will Hunting was portrayed more as a thug first, intellectual second (it was the reverse in real life). In real life, the psychologist he was to see was his father, Boris Sidis. Now, isn’t that a tad, shall we say, unethical? Exactly what was to be the outcome here? The only way you can be clinically objective about your own son is to not have feelings for your son at all, and doesn’t that defeat the purpose of therapy in a rather deep and profound way? I guess one way to become screwed up is to have issues with your father; and one way to be really screwed up is to have that same father for your therapist. NOOOOOOOO!, I can hear him screaming. Ah, but I digress.

No one doubts that Sidis was a prodigy. But what of the number given to him: 250 – 300, which pretty much isolates him from the rest of humanity (even going back to the dawn of antiquity)  as an intellectual? Is this number even meaningful? Is it legitimate? An IQ like that would make him “smarter” than Leonardo da Vinci, or Michelangelo. Even Albert Einstein had to give the world his special and general relativity theories while chugging along with his meagre 205 IQ.  On this scale, Isaac Newton was an also-ran; and Galileo could be arrogant to the Pope, but like John The Baptist, he should not feel himself fit to tie the sandals of someone on the scale of Good Will Sidis, apparently.

Will Sidis, as far as history can tell, is just known for being smart; he didn’t contribute anything, except for this “human thermodynamics/entropy reversal” stuff, which few have heard of. His contribution doesn’t seem as all-encompassing as Einstein or Michelangelo, so having the IQ score alone is nothing to be envious about. Nearly all of those slowpokes who meandered to their historical achievements had to do so while galumphing along with the humble 190-210 IQs that God gave them, if we are to believe the posthumous IQ scores given to them.

Visits: 75

The Psychology Contrarian I: The obsession with IQ

When there are no serious researchers that would place any relevance on our current obsession with IQ and what it measures (indeed, what exactly is it measuring is itself a mystery: does intelligence even have a definition, or am I missing out on something?), I wonder why there are web sites which even go so far as to go back in history, centuries before there were IQ tests or even a field of psychology as we know it, and begin to assign IQs to people like Michelangelo, Leonardo da Vinci, Aristotle, Hypatia, Isaac Newton, and so on, as if we were handing passing out candies, albeit to dead people.

I think IQ is the last bastion of that age where math was taken too seriously, and secret societies were formed out of assigning numbers to strange and abstruse things. The IQ, much like saying “chair = 5”, was and is the last of these to fall. The same care and attention given to assigning numbers to daffodils and planets is being given to historical figures who had never seen, heard of, or taken these tests. It forms an easy method by which we can feel we understand the world without having to go through all the bother of reading of people’s biographies or accomplishments, or knowing anything about them at all. Their entire intellectual and scholastic oeuvre can be summarized in a three-digit number, and that’s all that matters to those of us who are IQ-obsessed.

One such person who was IQ obsessed was Rick Rosner, whose first IQ test was about 150, but repeatedly took more tests such that his IQ was inflated to 170 to 190. He said in an interview that 150 was OK for being the smartest in your high school, but not OK for being the smartest person at a place like Harvard. A 150 IQ just sort of blends in.

Of course, this logic fails because it confuses IQ scores with achievement. There is more to life than smarts; of course we can all do with more of it. The main ingredient, and possibly the most important ingredient leading to achievement and success in life is self-efficacy. Self-efficacy is the ability to make manifest the goals you set. Self-efficacy takes focus, determination, and discipline. These are things well within the reach of any average person.

Visits: 125

Zero

Once upon a time, around the year 525 during the reign of Pope John I, a monk named Dionysius invented the idea of Anno Domini by producing a calendar which marked the time since the birth of Christ. The numbering of the years was adopted for the Julian Calendar, a calendar created 600 years previous under the reign of Julius Caesar. The Julian Calendar allows for 12 months, 365 days per year, and 366 on leap year, once every 4 years. The numbering of the years would change with Anno Domini.

The calendar lost 11 minutes per solar year, then over time, 3 entire days out of every 400 years, so that by 1582 under Pope Gregory, a new calendar was issued that made that correction. Now, under what is known as the Gregorian Calendar, a leap year will happen every 4 years, and on years divisible by 400; but not on years divisible by 100. 1900 was not a leap year, but 2000 was.

But there was a bigger problem in the concept of Anno Domini. There was no year zero. A kid born on 1 BC would be 3 years old by 3 AD. But if you subtract, you get the wrong answer: 3 − (-1) = 4, and this is because there is no year zero in the calendar. For the Dionysian calendar, the counting is: -1, 1, 2, 3, rather than -1, 0, 1, 2, 3. The blame cannot be laid at the feet of Dionysius alone, however. Dionysius did not know of the number zero, because the number had not been known to the Romans, nor the Greeks, and not even the Church, for hundreds of years.

Well, it kind of did. The Arab world had known and used the number in their counting system since at least the days of the Greeks, and possibly before. Aristotle stated that there was no such a thing as a vacuum, and thus the very idea of zero, or of “nothing” as being countable, was anathema to Greek philosophy. Greek geometry, with all of its laws and proofs,  had to proceed without it. They were aware that zero was being used by the Babylonians, but the Greeks had a good thing going with their pursuit of philosophy and didn’t want it being messed up by the introduction of zero.

This meant that the Romans, who did not pursue philosophy so much, had no zero in their rather cumbersome number system. And the Catholic church, who embraced Aristotle, had no zero for hundreds of years, and didn’t even question Aristotle’s idea of a vacuum until the 13th century. While the Catholics liked a rational God, and pursued philosophy and mathematics in their monasteries during the so-called “Dark Ages”, and even started the university system some time after the 10th century, did not see until much later how zero could actually fit in with their theology regarding “the void” and “the infinite”.

In the meantime, a calendar had been produced that had no year zero. This meant that centuries do not begin at multiples of 100, they have to begin at 100 + 1. While everyone was euphoric over the year 1999 becoming the year 2000, really the 21st century didn’t begin until 2001.

Visits: 96

A reluctant technophile disses cell phones

I like the latest technologies as much as anyone. As I type this, I am using a Bravia hooked up to a quad-core PC using an HDMI cable, and have it hooked up to the ‘net with a wi-fi connection. And I know that most of my equipment can’t be bought new anymore. I have always realised that it is hopeless to keep up with the latest developments, or even to keep up with the news of it.

I like to choose my technologies carefully, for things that really make my life easier, saving work, time, and money. For me, devices have to do more than just look flashy.  I never lock into long-term contracts with cell phones, and like the idea of “unlocked” cell phones. I think control over a device that you paid for is a human right, and it is the only decent thing to do with a device that a user purportedly owns. A cell phone shouldn’t own you. Or “pwn” you, to be more precise. Most of these cell phones are made of delicate plastic, with large glass touch screens that could not survive a drop of 3 feet. You might drop your phone at least once in that time, meaning for part of the life of your 3-year contract, you’re stuck paying for a phone that is no longer useable, while you have to go pay for another one. If that isn’t financial enslavement for inferior-quality devices, nothing is.

Visits: 94

Recreational Math I: Magic Squares: the “really good” kind – Part 6

Welcome to part 6, where the magic squares are 7×7. 7 was the number of known planets in medieval times, as well as the number of known elements, and the number of days in the week. The rest is all alchemy.

The algorithm for a 7×7 matrix is the same as for 5×5. In fact, it should work for any odd prime-ordered matrix. Do the first based on a random sequence of the numbers between 1 and 7:

1 6 2 3 4 7 5
7 5 1 6 2 3 4
3 4 7 5 1 6 2
6 2 3 4 7 5 1
5 1 6 2 3 4 7
4 7 5 1 6 2 3
2 3 4 7 5 1 6

Now, do the second matrix using 0 and every seventh number after it up to 42:

7 42 0 21 14 35 28
0 21 14 35 28 7 42
14 35 28 7 42 0 21
28 7 42 0 21 14 35
42 0 21 14 35 28 7
21 14 35 28 7 42 0
35 28 7 42 0 21 14

The resulting matrix is magic, but not “hyper-magic” like the 5x5s were:

8 48 2 24 18 42 33
7 26 15 41 30 10 46
17 39 35 12 43 6 23
34 9 45 4 28 19 36
47 1 27 16 38 32 14
25 21 40 29 13 44 3
37 31 11 49 5 22 20

The matrix above was done using Excel, and checked using VBA, where I checked it for “magic”. The loss of hypermagic is unfortunate, but I suppose inevitable when you scale up. There are (7!)2 = 25,401,660 magic squares possible by this algorithm. The VBA proved handy later when I used dynamic programming to produce any odd-ordered magic square of any size, and investigated the results.

What if I made a mistake and got the shifting wrong, such as shifting from the second number from the left instead of the right? The result is variable; full magic can only be restored if the rightward diagonal is all 4/s:

7 3 6 2 5 1 4
3 6 2 5 1 4 7
6 2 5 1 4 7 3
2 5 1 4 7 3 6
5 1 4 7 3 6 2
1 4 7 3 6 2 5
4 7 3 6 2 5 1

Why does this work? This is because the sum of the numbers 1 to 7 in any order is 28. Notice that whatever number is in the opposite diagonal is repeated 7 times. There is only one number, when multiplied by 7, equals 28, and that is 4. All other numbers will result in a loss of magic. This appears to be a way to maintain magic in all odd-ordered magic squares past order 7. This can possibly generalize for squares of prime order n by taking the middle number (n+1)/2 and making it the main diagonal.

When added to the second preliminary square, both diagonals became magic, as well as the columns and rows. But because the opposite diagonal consists of all 4’s, we lose variety with this restriction, but not by much: 7!6! = 3,628,800. Still enough to occupy you on a rainy day.

9×9 magic squares won’t work so well, because the second square is shifted by 3, which is a number that divides 9. This will result in certain rows repeating in one of the pre-squares; and the result generally is that one of the diagonals won’t total the magic number (369 in this case).

13 66 78 59 27 8 34 38 46
74 55 22 3 33 41 54 17 70
26 7 29 37 49 12 69 77 63
32 45 53 16 65 73 58 21 6
48 15 68 81 62 25 2 28 40
64 76 57 24 5 36 44 52 11
61 20 1 31 39 51 14 72 80
9 35 43 47 10 67 75 60 23
42 50 18 71 79 56 19 4 30

This is a consequence of 9 not being a prime number. The algorithm that works so well for 5×5 and 7×7 magic squares breaks down when the odd number is composite. Thus, the algorithm is known to work for 11×11, 13×13, 17×17, and has been tried all the way to 101×101 and beyond on my Excel spreadsheet.

The magic number can be known in advance of any magic square because an order-n magic square obeys the formula (n × (n2 + 1))/2. The best bet is to look for odd-ordered n × n squares where n is prime. In my VBA program, I made double sure by sticking to magic squares where the order is prime. Here is an 11 × 11 square, where the magic number is 671:

112 20 60 87 3 41 92 33 105 51 67
62 78 2 42 93 32 102 52 70 121 17
11 39 95 23 101 53 71 120 14 63 81
96 26 110 50 73 111 13 64 82 10 36
109 47 74 114 22 61 84 1 35 97 27
75 115 21 58 85 4 44 94 29 100 46
12 57 86 5 43 91 30 103 55 72 117
83 7 34 90 31 104 54 69 118 15 66
37 99 28 106 45 68 119 16 65 80 8
25 107 48 77 116 18 56 79 9 38 98
49 76 113 19 59 88 6 40 89 24 108

Finally, to stretch things out to the boldly absurd, what about an order-23 square whose magic number is 6095?

92 369 279 275 108 466 226 403 125 327 360 316 55 457 485 14 192 182 234 425 36 145 524
283 271 115 461 210 413 131 328 364 311 56 442 498 17 193 181 232 428 31 159 510 80 381
103 473 214 409 138 323 348 321 62 443 502 12 194 166 245 431 32 158 508 83 376 297 257
228 395 126 335 352 317 69 438 486 22 200 167 249 426 33 143 521 86 377 296 255 106 468
129 330 366 303 57 450 490 18 207 162 233 436 39 144 525 81 378 281 268 109 469 227 393
365 301 60 445 504 4 195 174 237 432 46 139 509 91 384 282 272 104 470 212 406 132 331
63 446 503 2 198 169 251 418 34 151 513 87 391 277 256 114 476 213 410 127 332 350 314
488 15 201 170 250 416 37 146 527 73 379 289 260 110 483 208 394 137 338 351 318 58 447
196 171 235 429 40 147 526 71 382 284 274 96 471 220 398 133 345 346 302 68 453 489 19
236 433 35 148 511 84 385 285 273 94 474 215 412 119 333 358 306 64 460 484 3 206 177
45 154 512 88 380 286 258 107 477 216 411 117 336 353 320 50 448 496 7 202 184 231 417
507 72 390 292 259 111 472 217 396 130 339 354 319 48 451 491 21 188 172 243 421 41 161
386 299 254 95 482 223 397 134 334 355 304 61 454 492 20 186 175 238 435 27 149 519 76
266 99 478 230 392 118 344 361 305 65 449 493 5 199 178 239 434 25 152 514 90 372 287
464 218 404 122 340 368 300 49 459 499 6 203 173 240 419 38 155 515 89 370 290 261 113
399 136 326 356 312 53 455 506 1 187 183 246 420 42 150 516 74 383 293 262 112 462 221
324 359 307 67 441 494 13 191 179 253 415 26 160 522 75 387 288 263 97 475 224 400 135
308 66 439 497 8 205 165 241 427 30 156 529 70 371 298 269 98 479 219 401 120 337 362
452 500 9 204 163 244 422 44 142 517 82 375 294 276 93 463 229 407 121 341 357 309 51
10 189 176 247 423 43 140 520 77 389 280 264 105 467 225 414 116 325 367 315 52 456 495
180 242 424 28 153 523 78 388 278 267 100 481 211 402 128 329 363 322 47 440 505 16 190
430 29 157 518 79 373 291 270 101 480 209 405 123 343 349 310 59 444 501 23 185 164 252
141 528 85 374 295 265 102 465 222 408 124 342 347 313 54 458 487 11 197 168 248 437 24

That probably ran into the neighbouring columns, but it’s just for illustration. The code, which I have used to generate magic squares of as high an order as 113 (magic number 721,505) is fewer than 170 lines in VBA for Excel 2007. And yes, even the above square, and the order 113 square are magic.

Visits: 152

A Little Late to the Party: The B. S. Generator

Yes, Bulls**t generator technology in its many forms and guises such as this site, using a cutting-edge convergence of certain verbs, nouns, and adjectives, has assembled compelling verbal deliverables using distributed front-end generators and extensible, enterprise-level methodologies to merge words into a confluent, innovative  passage of meaningless web content. See how I am e-enabled to author difficult and dense passages of the simplest mental models and efficiently interface these paradigms, internetworking un-necessary deadwood phrases and hackneyed clichés with tired jargon, into a customised, extensible, Web 2.0-ready piece of killer content reminiscent of a squid squirting ink.

As the title suggests, I have only discovered these BS generators recently, but the technology itself seems to have been in common availability on the web since the early 2000s. It’s fun to write, but difficult to do if you actually want to make a point.

Visits: 83

Recreational Math I: Magic Squares: the “really good” kind – Part 5

I have met with some disappointment as to how a methodology for creating a 4×4 square should pan out, and instead I have come up with many different algorithms, each resulting in its own small sets of magic squares, but had stumbled upon a set of squares with similar “hyper-magical” properties which I called the Durer Series.

I had met with some disappointment at this, and am still in the middle of writing my own 4×4 square program in Visual Basic .NET (it’s going to use a “brute force” algorithm … sorry!). With that, I had to learn about how .NET does objects. To those of you out of the loop on the recent .NET versions of VB, this language actually allows you to create your own novel objects, thus saving processing time if the right kind of objects are created. It’s a work in progress.

For now, I wanted to centre on the pièce de résistance of this series: that of the odd-ordered magic squares, those of order 5 and beyond. But it can’t just be any odd number. For the algorithm to work, the order of the square has to be a prime number greater than 5. As I hinted at the beginning of this series, these are special and unique in that an algorithm can be made for an order-n magic square (where n is an odd prime) which can generate (n!)2 squares, all magic (even after weeding out duplicates, the numbers of unique squares will still be in the thousands).

This seems to be a hard-to-find algorithm, except from a book called The Fascination of Numbers, written on the year of The Queen’s coronation in 1957 by W. J. Reichmann while he was still a headmaster at a Grammar School located in Spalding, Lincolnshire, England (according to my signed copy of the book, purchased from an English vendor through Amazon used books). I read it for the first time at a university library, and it is likely to be found in a similar univeristy or college collection near you.

What I like about this algorithm is that while I have used it to write computer programs for magic squares, it really requires no more than pencil and paper, and a bit of skill at addition.

First of all, write down the numbers from 1 to 5, in any order at all:

3, 2, 1, 5, 4

A 5×5 square matrix is constructed in a pattern by starting from the fourth number in the sequence, then proceeding with the 5th number, then the first, second and finally the third:

4 2 1 5 3
5 3 4 2 1
2 1 5 3 4
3 4 2 1 5
1 5 3 4 2

Next, scramble the first 5 multiples of 5 (counting 0):

20, 0, 5, 15, 10

Create a 5×5 matrix by shifting the order of these numbers by 2 to the left as follows:

20  0  5 15 10
 5 15 10 20  0
10 20  0  5 15
 0  5 15 10 20
15 10 20  0  5

Now add them together, adding together numbers located in the same columns and rows in both squares, as in matrix addition:

24 2 6 20 13
10 18 14 22 1
12 21 5 8 19
3 9 17 11 25
16 15 23 4 7

The result is a magic square which has many more ways of obtaining  the magic number 65 than just adding the rows, columns, and diagonals. Taking any 3×3 sub-square on the corners or left/right sides of this square and adding its corner numbers to the middle number will obtain 65. This seems to be true of all magic squares made by this method. Since both squares can be scrambled independently, there will be (5!)2 = 14,400 possible squares before duplicates are weeded out. I have written programs in many languages regarding this 5×5 square, and can attest to the robustness of this algorithm in producing a nearly endless series of 5×5 magic squares, all sharing very similar “magical” properties.

Reichmann also reminds us that the scrambled 5×5 squares we created initially are also magic.

I suspect there may be more than 14,400 magic squares. Are there any squares that cannot be produced by this algorithm? This must be checked against a “brute-force” (read: computational) method for generating all possible magic squares to see if this is really the definitive number. It is certainly a couple of orders of magnitude greater than what Danny Dawson did with his 4×4 squares (around 920 squares or so, with some duplicates). It would also be interesting to know what squares could not have originiated from Reichmann’s algorithm (proven by working backwards to show, supposedly, that duplicate numbers appear in some rows of the first or second matrix, which disappears in the resultant matrix.

It also seems that 4×4 and 5×5 squares can have such “compound” magical properties; it is harder to find for 7×7 matrices, although they are additive to the magic number in just enough ways so as to say they are magic. We’ll leave that for the next journal entry.

Visits: 91

Recreational Math I: Magic Squares: the “really good” kind – Part 4

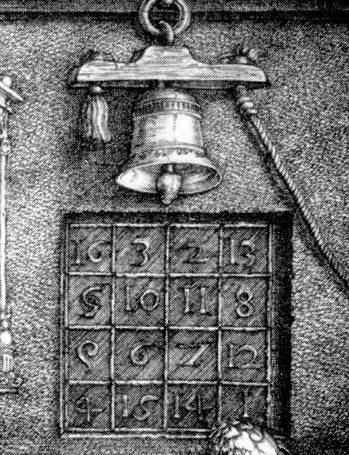
How to Make a Random Square

I have noticed that it has been difficult to elucidate a method for systematically creating even-ordered magic squares of any but the most basic kind. I don’t know why this is, since the art has been alive in Europe for at least 600 years, and probably longer in other cultures. There are a few methodologies out there, but they are perfunctory. Such as, this method offered by Reichmann (1957), which tells us little more than to write the numbers down from 1 to 16 and reverse the order of the diagonals:

 1  2  3  4        16  2  3 13
 5  6  7  8  ====>  5 11 10  8
 9 10 11 12         9  6  7 12
13 14 15 16         4 14 15  1

Well, only a limited number of magic squares are possible that way. You can reverse the order of the numbers, or write the numbers in order down the columns instead of the rows, followed by a similar reversal of the diagonals (these would not be considered to be unique solutions, since these methods amount to mirroring or rotating the square).

After some playing around with known 4×4 magic squares (thanks to the thorough resource offered here), and using some simple rules, I think I may have come upon a method on my own. I would suppose that it could not generate all magic squares possible, but I don’t intend to offer a complete solution. I estimate that I would be able to generate maybe another 10 or so magic squares with this method. The intent here is to allow the reader to create a 4×4 magic square sitting down at a table with little more than pencil and paper. I am sure this methodology is published elsewhere, but I wasn’t able to come up with anything.

I just have a few simple rules in coming up with the method. First of all, all of the 16 numbers are the result of a sum of two smaller numbers a and b, where a is a number from 1 to 4 such that a = {1, 2, 3, 4}, and b is a multiple of 4: b = {0, 4, 8, 12}. All 16 unique numbers generated will be the result of adding a number from set a to a number in set b.

The numbers 1, 2, 3 and 4 are the result of adding set a to 0 in set b.

The numbers 5, 6, 7, 8 come from adding set a to 4 in set b.

The numbers 9, 10, 11, 12 come from adding set a to 8 in set b.

And the numbers 13, 14, 15, 16 come from adding set a to 12 in set b.

My solution is inspired by Reichmann’s (1957) work on odd-ordered matrices. This solution on even-ordered matrices is quite different than for odd-ordered matrices, but the idea of adding two matrices and getting a magic square appealed to me, so I went with that basic idea.

The first matrix uses numbers from set a, in the following pattern:

4  3  2  1
1  2  3  4
1  2  3  4
4  3  2  1

These numbers may be randomized, but I’ll just stick to numeric order for now. The second matrix is composed of the numbers of set b arranged in a pattern reminiscent of the Durer square:

12  0  0 12
 4  8  8  4
 8  4  4  8
 0 12 12  0

The sum of the two matrices has all the magic of the Durer square, and consist of the unique numbers 1 to 16:

16  3  2 13
 5 10 11  8
 9  6  7 12
 4 15 14  1

In fact, it is the Durer square itself. Now that we know it works, what about mixing things up? Take note of the patterns. Let the first matrix represent numbers {a, b, c, and d} belonging to set a; and {e, f, g, and h} belonging to set b. whatever randomization is chosen, the numbers must fit the following scheme:

a  b  c  d      e  h  h  e
d  c  b  a      f  g  g  f
d  c  b  a   +  g  f  f  g
a  b  c  d      h  e  e  h

a, b, c, and d may be any permutation of the numbers 1 to 4, without apparent limitation. The second and third rows on teh first matrix are the reversals of the first and fourth. The second matrix, however is much more restricted. Considering e and f to be one pair; g and h to be another pair: 12 can only be paired on the same row with 0; and 4 only be paired with 8. Otherwise, no joy.

So, on with a randomized square: let a = {3, 1, 4, 2} and b = {8, 0, 12, 4}

3  1  4  2     8  4  4  8     11  5  8 10
2  4  1  3     0 12 12  0      2 16 13  3
2  4  1  3  + 12  0  0 12  =  14  4  1 15
3  1  4  2     4  8  8  4      7  9 12  6

What about a = {2, 4, 1, 3}, and b = {4, 12, 0, 8}

2  4  1  3      8  4  4  8     10  8  5 11
3  1  4  2     12  0  0 12     15  1  4 14
3  1  4  2  +   0 12 12  0  =   3 13 16  2
2  4  1  3      4  8  8  4      6 12  9  7

You may also treat sets a and b oppositely, while randomizing. This time the restriction is on matrix a — 4 pairs with 1, and 2 pairs with 3:

3  2  2  3     8 12  0  4     11 14  2  7
4  1  1  4     4  0 12  8      8  1 13 12
1  4  4  1  +  4  0 12  8  =   5  4 16  9
2  3  3  2     8 12  0  4     10 15  3  6

The reason I say these squares are limited to about 10 or so, is because as you can see, the individual rows or columns end up being about the same — at best, a shuffling or reversal the same rows found in the Durer square. There are at best 24 such squares, not subtracting tilted (squares the same when laid on its side) or reflected squares (where the squares are mirror images of each other). All that might be said, is that we may have discovered all the ways a magic square may be constructed with the same “hyper-magic” as the Durer square, which may be a pretty cool thing to say actually. It’s just that my goal was more ambitious at the start. I will refer to the set of 4×4 hypermagic squares built on the same rules as “the Durer series.”

Any known magic square, however, is the result of a unique combination of the basic squares built on sets a and b. Respectively, I will call the matrices A and B.  This allows us to work backwards from a 4×4 square we know is magic, and discern any patterns. The above squares were done that way. What patterns can be observed for the following square, which this website offers as #379 out of 900 or so others?

                Matrix "A"      Matrix "B"
13 12  6  3     1  4  2  3     12  8  4  0
10  5 11  8     2  1  3  4      8  4  8  4
 7 16  2  9  =  3  4  2  1  +   4 12  0  8
 4  1 15 14     4  1  3  2      0  0 12 12

One may discern a pattern here, but it is not all that obvious, especially for the square built on set b. It doesn’t seem to resolve itself into simple rules and patterns the way the Durer series of squares did. Also, you might have noticed that this square is not quite as “magic” as the Durer series, though all rows, columns, and both diagonals give you 34.

But I do notice that in matrix A the last column is a reversal of pairs of the first column. Also, the third column is built on the middle numbers of the first column, and the second column are built on the middle numbers of the last column.

What of Matrix B? The first and last columns are reversals (of all 4 numbers, not of pairs), the second and third both start with the middle two numbers, then first, then last from their adjacent end columns: “e f g h” becomes: “f g e h”.

When I tried to build on these rules, I got duplicate numbers in my squares (and with that, some missing numbers). It would appear that the observable number patterns in such squares are limited to getting you maybe 4 to 8 unique squares, then you have to make a new set of rules each time. With over 900 squares discovered (give or take a duplicate or two), that’s a lot of rules. The total number of 4×4 squares, both magic and not, are equal to 16! = 21 trillion possible squares. Finding all possible magic squares, weeding out any duplicates, reflections, and sideways duplicates would seem a tad non-trivial. Even at the website I referred to for these squares, it has been shown that the number “924” claimed as the number of possible 4×4 magic squares, might be too high, due to some duplicates found. Their scripts took just under 25 seconds to generate and check these squares — but just to check them for magic, less so for duplication, which sounds like it would take more computer time.

Visits: 111

Recreational Math I: Magic Squares: the “really good” kind – Part 3

Notice that to show the rules for making these kind of magic squares, I used only odd-ordered square matrices as examples. What about matrices of even numbers of rows and columns? The rules for these vary.

A detail from Albrecht Durer's Melancholia engraving
This is a small part of a 1514 engraving by Albrecht Durer, called Melancholia. The author of the article that houses this graphic asserts that there are 32 possible 4×4 magic squares with the famous pun “1514” in the same position as above. This magic square has a symmetry in the numbers, as explained below.

The famous Durer magic square, with the year of the engraving cleverly made a part of a magic square, has a certain organization in its construction, as well as a certain symmetry. The numbers are constructed, in sequence:

_   3   2   _        _   3   2   _
_   _   _   _        5   _   _   8
_   _   _   _  ====> _   6   7   _
4   _   _   1        4   _   _   1         

_   3   2   _       16   3   2  13
5  10  11   8        5  10  11   8
9   6   7  12  ====> 9   6   7  12
4   _   _   1        4  15  14   1

So, you start from the bottom right and proceed in a horseshoe to the top then the bottom left. The next diagram places the numbers 5-8 in a pattern that is left-to-right u-shape. Then the same u-shape for the numbers 9-12 from left to right, except this time it’s upside-down. Finally ending as we started, the same horseshoe shape (except right side up) from right to left.

Durer’s square has many things about it, apart from its magic number (34) which works on all the attendant diagonals, rows and columns. The middle 4 squares add up to 34 (10 + 11 + 6 + 7 = 34); the four corners add to 34 (16 + 13 + 4 + 1 = 34), and all corner foursomes add to 34: (16 + 3 + 5 + 10); (2 + 13 + 11 + 8); (9 + 6 + 4 + 15); and (7 + 12 + 14 + 1).

The numbers at the ends of the two middle rows add to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

and the numbers at the tops and bottoms of the two middle columns add to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

If we take another symmetrical combination: a rightward-slanting rectangle whose corners are 2, 8, 9, and 15, these also add to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

The leftward-slanting rectangle, whose corners are 5, 3, 12, and 14 also add to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

Starting from 2 and proceeding in an “L”-shape to the left to the number 5, and continuing counter-clockwise in the same manner gets us the corners of a tilted square whose numbers 2, 5, 15, and 12, add to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

Starting from “3” and doing likewise yields the numbers 3, 9, 14, and 8, also adding to 34:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

And what about this talk about “symmetry”? By this, we mean that we may take pairs of numbers at the start and end of any row, and they add up to the same number in a symmetrical place elsewhere. 16 + 3 = 4 + 15, taking the top and bottom of the first and second column. Likewise can be done for the last two columns: 2 + 13 = 14 + 1. The middle two rows have the same property: 5 + 10 = 9 + 6; and 11 + 8 = 7 + 12. On a larger scale, the sums of the middle two rows of columns 1 and 2 are the same as the tops and bottoms of columns 3 and 4: 11 + 8 = 7 + 12 = 16 + 3 = 4 + 15. Likewise, the sums of the middle two rows of columns 3 and 4 are the same as the tops and bottoms of columns 1 and 2: 2 + 13 = 14 + 1 = 5 + 10 = 9 + 6. These two groups of symmetrical numbers are illustrated below in red and green:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

The sums of 15 (green) and 18 (red) across each row form this pattern

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

The downward symmetry is also interesting. Here, the sum of 25 is in gold and the sum of 9 is in blue. In the process, we can discern the patterns that we used to construct the square in the first place:

16   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

This is an incredible amount of magic, but if you follow the order of filling (horseshoes are right-to-left, u-shapes are left-to-right, along with the peculiar pattern of filling u’s and horseshoes), there really are four possible patterns that have these “hyper-magic” qualities, but you lose the “1514” idea in two of them:

 8  11  10   5      12   7   6   9       4  15  14   1
13   2   3  16       1  14  15   4      12   6   7   9
 1  14  15   4      13   2   3  16       5  11  10   8
12   7   6   9       8  11  10   5      16   3   2  13

Of course, you could reverse all of the numbers in the rows of the first two squares to get your “1514” back.

Every time I look at that darned Durer square, I keep seeing more patterns. I think there comes a point where one has to leave the remaining observations up to the reader.

There is yet another 4×4 square, and with it we can increase the magic, if that can even be conceivable after all I have said. But there is a square with even more magic than the Durer square. R. J. Reichmann mentioned it in his book “The Fascination of Numbers”, first published in 1957. The square could be constructed like this:

-  -  3  -        -  -  3  6        - 10  3  6        15 10  3  6
4  -  -  - ====>  4  5  -  - ====>  4  5  -  9  ====>  4  5 16  9
-  -  2  -        -  -  2  7        - 11  2  7        14 11  2  7
1  -  -  -        1  8  -  -        1  8  - 12         1  8 13 12

This square has all the magic of the Durer square and then some. One thing this new square has over the Durer square is that any four numbers in square formation will add to 34, from anywhere in the square. These include the foursomes:

10  3     16   9     11   2       4   5
5  16      2   7      8  13      14  11

Visits: 86

Recreational Math I: Magic Squares: the “really good” kind – Part 2

Last time I introduced the idea of magic squares. I promised I would show you how to make one. In this post, I will begin by discussing “trivial” squares, or squares made by simple rules of following diagonals and wrapping.

When I say a square is “magic”, I mean that all rows, columns, and diagonals add up to the same number. While other sources, such as Wolfram’s Mathematica, say that only the main diagonal of the matrix need be magic, I will take the more strict requirement that both leftward and rightward diagonals have to be magic.

There are trivial magic squares that begins by following a rule where you start with “1” in the top middle square, then move up and to the right one square, and place a “2” there.

_  1  _
_  _  _
_  _  _

But you may have noticed that if you start at the top, how can you move “up and to the right”? You get around this by “wrapping” to the bottom, treating the bottom of the rightward column as though it is above.

_  1  _
_  _  _
_  _  2

OK, you say, but now there’s no “right” after the last column. Now what? Now you can wrap so that the leftmost column is treated as “right of” the rightmost column:

_  1  _
3  _  _
_  _  2

Now another problem: up and to the right of “3”, there is a “1” in the way. If this happens, you are allowed to place the fourth number below the “3”:

_  1  _
3  _  _
4  _  2

Now, following these rules and exceptions, we can keep going:

8  1  6
3  5  7
4  9  2

The result is a magic square whose rows, columns and diagonals add up to 15.

I found that if I moved the 1 elsewhere and followed these rules in the same manner, some or all of the “magic” is lost. There seems to be only one magic square that can be made using these rules, at least one that adds up to 15 in all of its rows, columns and diagonals. The following 3×3 magic squares were the closest I could come to any credible “magic” by placing the “1” in a different position:

6  8  1                4  9  2
7  3  5 and similarly: 8  1  6
2  4  9                3  5  7

But notice in both cases, neither of the diagonals add up to 15. In the next post, I will discuss a way to break this limitation, making it possible to construct up to 36 3×3 magic squares.

Meanwhile, let’s expand the idea to 5×5, using the same, identical rules. This one seems easier in a way, since there aren’t as many blockages early on:

17  24   1   8  15
23   5   7  14  16
 4   6  13  20  22
10  12  19  21   3
11  18  25   2   9

I particularly like 5×5 squares. But my experience with placing the “1” elsewhere than the exact middle position of the top row has resulted in a loss of “magic”. However, I was lucky on my first attempt with moving the “1” around. The following magic square has a “Mathematica” level of magic:

11  18  25   2   9
17  24   1   8  15
23   5   7  14  16
 4   6  13  20  22
10  12  19  21   3

Later in this series, we can break this limitation, too. But next, we shall discuss some 4×4 magic squares, including one that made history.

Visits: 79

Recreational Math I: Magic Squares: the “really good” kind

Introduction

ONE OF THE few things you see on the web these days is how to do a really good magic square. There are many websites that tell you about how spiralling arrangements of sequential numbers on a square matrix is magic, but for me, that’s dull. You are limited to doing seemingly less than a dozen such magic squares, so I don’t find them too interesting.

Recall that magic squares are numbers arranged in a square matrix such that each of its rows and columns, and normally both diagonals add up to the same number. Usually, a square of n numbers to a side which has numbers total, will be populated with the entire set of numbers from 1 to n inclusive, in some quasi-random order. These numbers would be arranged in such a manner that the total of each of its rows, columns, and both diagonals equal the same “magic number”, which is different depending on the dimensions of the square. By using random methods suggested in this article, the number of magic squares possible, when n is odd, is equal to (n!)2.

For the 5×5 square, you apparently have to start by moving from the current position to the “top right” square (wrapping to the opposite edge if necessary), and if that square is occupied, move down by 1 square. This non-random, deterministic method apparently works for all squares greater than 5×5 (with odd dimensions).

I read from an old book on recreational math (The Fascination of Numbers, by W. J. Reichmann (1958)), that

  1. Squares of even dimensions (4×4, 6×6) have to be arranged by a different algorithm than squares of odd prime dimension (5×5, 7×7, 11×11, …).
  2. A randomly-generated 5×5 magic square can be made which uses the sum of two matrices.

The number of possible permutations of 5×5 matrices is equal to (5!)2.

Reichmann’s book was the only place where I could find such an algorithm. This seems to be a rare algorithm, even on an internet search. But it is the only method that leads to “magic” results in a variety of ways. These squares seem to be the most robust in terms of the number of ways their “magic” qualities can be determined. They have inspired my writing computer programs that generate such squares as a way of practicing programming several years ago. I have written magic square programs following Reichmann’s algorithm (not sure if he originated it) in VB5, Visual Basic .NET, VB for applications (in Excel), and in Microsoft Quick Basic 4.5. The 16-bit QB 4.5 version does not run on my 64-bit machine, and for similar reasons, neither does the VB5 version, whose runtime DLL is no longer supported by MS Windows 7.

In the next instalments, starting this coming Saturday, I will begin to discuss the making of 3×3 and 5×5 squares, and discuss their magic properties.

Visits: 100

Getting f(x) notation to work in Maple

Maple is a robust math environment which can graph, solve equations, and solve for the unknown with the aid of its computer algebra solver (CAS), which is capable of computing exact roots of cubic functions, for example.

I wanted to demonstrate for myself that Maple could do various function transformations, such as: f(x), f(x + 1), f(x) + 1, 2*f(x), and the like. I discovered after much reading and browsing the web that I could coax f(x) to do whatever is needed using an inline call:

f := proc (x :: float) option inline;
x4 + 5x3 + 5x2 - 5*x - 6
end proc:

The function takes a floating point number x as a parameter. This means that f(-10.0) would yield

5544.0000

as output. I noticed that Maple practices fairly strong typing, so if you declare floating point using float, you can only pass floats to the function. That is, f(-10) would have gotten an error, at least in my copy of Maple 12. Once you execute this proc declaration, you can do a plot function like:

plot ({f(x), f(x + 1), f(x + 2)}, x = -5..5, numpoints=1000);

and superimpose three curves on the same set of axes to make a comparison. You can even do:

plot ({f(x), 0.5 * f(2*(x + 1)) - 5}, x = -10..10, numpoints=1000);

to illustrate combinations of transformations of a function. Even a transformation of a sine wave can look like this:

h := proc (x::float) option inline;
sin(x)
end proc;
plot(1.5h(2(x+Pi/4)), x = -2Pi .. 2Pi, numpoints = 5000, tickmarks = [spacing((1/4)*Pi), default]);

and you are rewarded with:

There is an even better function called animate which is great for transformations of functions. I will discuss that in a later post.

Visits: 91

And now a word from our sponsor

3 Funny PSAs, courtesy of Jacob Maymudes. A little on the tasteless side, but if you came to my site, I suppose you weren’t expecting Little Bo Peep. Which is not to say anything negative about Bo Peep, sheep or little girls as shepherds. Miss Muffett, another nursery rhyme, though, was a little edgier, since the plot involved a spider. Whatever, … so without further doo-doo:

#1 Time Machines

#2 Robots:

#3 Use Caution with hyperspeed

Visits: 61